
ทำไม "สมการออยเลอร์" จึงได้ชื่อว่า "สวยงามที่สุด" ในคณิตศาสตร์?
พาไปรู้จักกับสมการที่ถือว่ามีความงดงามที่สุดในคณิตศาสตร์คือ สมการออยเลอร์ (Euler's identity) ของ เลออนฮาร์ต ออยเลอร์ นักคณิตศาสตร์และนักฟิสิกส์ชาวสวิส และบุคคลแรกที่เริ่มใช้คำว่า "ฟังก์ชัน"
สมการออยเลอร์ นี้ก็คือ eiπ+1=0 ได้รับการยกย่องว่าเป็นสมการที่สวยงามที่สุด เพราะมันเชื่อมโยงกันระหว่างตัวแปรที่สำคัญที่สุดในคณิตศาสตร์ที่ดูเหมือนจะไม่มีความเกี่ยวข้องกัน แต่จริงๆแล้วมันมีความเชื่อมโยงที่ลึกซึ้งมาก
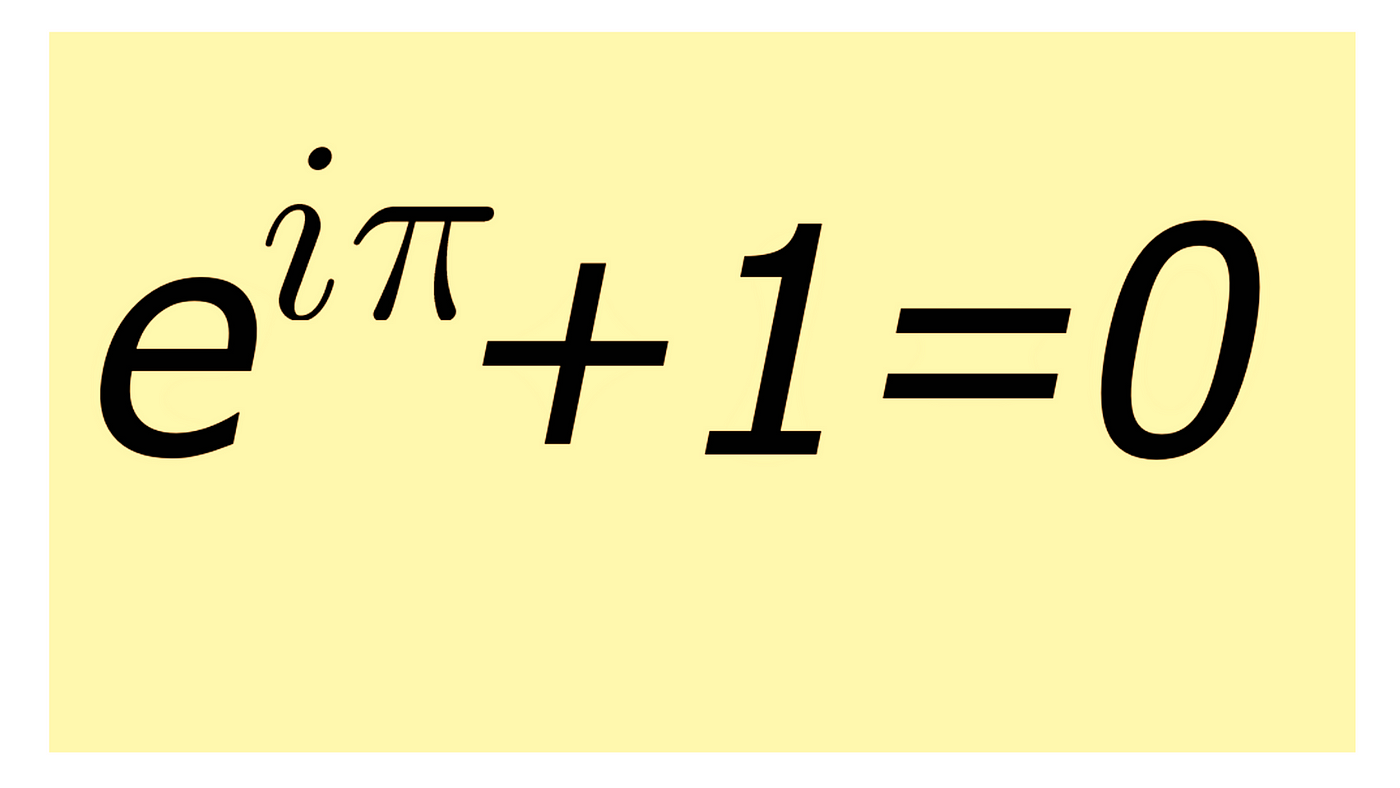
สมการนี้ประกอบไปด้วย:
- ee: ค่าคงที่ที่เป็นฐานของลอการิธึมธรรมชาติ (Natural Logarithm) ค่าของ ee เป็นตัวเลขที่ไม่จบไม่สิ้นและมีค่าประมาณ 2.71828 ซึ่งมีบทบาทสำคัญในสาขาคณิตศาสตร์หลายแขนง เช่น การวิเคราะห์ (Calculus) และทฤษฎีความน่าจะเป็น
- ii: หน่วยจินตภาพ (Imaginary unit) ซึ่งนิยามว่า i2=−1i2=−1 ค่าของ ii เป็นพื้นฐานสำคัญในการศึกษาของคณิตศาสตร์เชิงซ้อน (Complex Numbers) ซึ่งเป็นการขยายขอบเขตของตัวเลขไปสู่มิติใหม่
- ππ: ค่าคงที่ทางเรขาคณิตที่ใช้สำหรับการคำนวณวงกลม ซึ่งมีค่าโดยประมาณ 3.14159 เป็นค่าที่สำคัญมากในหลายสาขาของวิทยาศาสตร์ โดยเฉพาะในวิชาฟิสิกส์และวิศวกรรมศาสตร์
- 1 และ 0: ตัวเลขพื้นฐานที่สุดในคณิตศาสตร์ที่ใช้ในการคำนวณทุกประเภท
ทำไมมันถึง "สวยงามที่สุด" ในคณิตศาสตร์?
- การเชื่อมโยงที่ลึกซึ้ง: สมการนี้เชื่อมโยง คณิตศาสตร์ที่ใช้ในเรขาคณิต (เช่น ππ) เข้ากับ คณิตศาสตร์เชิงปริมาณ (เช่น ee และ ii) โดยที่ทุกส่วนของสมการล้วนมีความสำคัญในคณิตศาสตร์ แต่กลับแสดงในรูปแบบที่เรียบง่ายและสวยงาม
- ความเรียบง่าย: ถึงแม้ว่าจะดูเหมือนซับซ้อนจากมุมมองแรก แต่สมการออยเลอร์จริงๆแล้วเป็นสมการที่เข้าใจได้ง่าย และสามารถใช้ในการประยุกต์ในหลายๆสาขาของวิทยาศาสตร์ เช่น ฟิสิกส์, วิศวกรรมศาสตร์ และเศรษฐศาสตร์
- ความสำคัญในคณิตศาสตร์: สมการนี้เป็นหนึ่งในสมการที่สะท้อนถึงความเชื่อมโยงระหว่างหลายสาขาของคณิตศาสตร์ โดยเฉพาะในเรื่องของ การวิเคราะห์ทางคณิตศาสตร์, การทำงานกับตัวเลขเชิงซ้อน และ ตรีโกณมิติ
สมการออยเลอร์จึงถูกยกย่องว่าเป็น "สมการที่สวยงามที่สุด" ในโลกของคณิตศาสตร์ ด้วยการรวมเอาค่าคงที่ที่สำคัญและฟังก์ชันที่มีความซับซ้อนมารวมกันในรูปแบบที่เรียบง่าย แต่มีความลึกซึ้งในการทำความเข้าใจนั่นเอง